orapun: มกราคม 2012

วันพุธที่ 18 มกราคม พ.ศ. 2555

ลำดับ (Sequence)

ลำดับ (Sequence)
อดีตกลุ่มปีทาโกเรียนสร้างจำนวนเชิงรูปภาพขึ้น เพื่อแสดงความสัมพันธ์ระหว่างเรขาคณิตกับ เลขคณิต เช่น จำนวนเชิงสามเหลี่ยม และ จำนวนเชิงสี่เหลี่ยม

จำนวนเชิงสามเหลี่ยม 5 จำนวนแรก

จำนวนเชิงสี่เหลี่ยม 5 จำนวนแรก
จำนวนเชิงสามเหลี่ยม ได้แก่ 1, 3, 6, 10, 15, ... ซึ่งมีจำนวนมากมายนับไม่ถ้วน
จำนวนเชิงสี่เหลี่ยม ได้แก่ 1, 4, 9, 16, 25, ... ซึ่งมีจำนวนมากมายนับไม่ถ้วนเช่นกัน

จำนวนเชิงสามเหลี่ยม และ จำนวนเชิงสี่เหลี่ยม เป็น ตัวอย่างของลำดับ ที่เรียกว่า ลำดับอนันต์ (Infinite Sequence)
จำนวนเชิงสามเหลี่ยม 5 จำนวนแรก และ จำนวนเชิงสี่เหลี่ยม 5 จำนวนแรก เป็น ตัวอย่างของลำดับ ที่เรียกว่า ลำดับจำกัด (Finite Sequence

ใน

วันเสาร์ที่ 14 มกราคม พ.ศ. 2555

ในการคิดคำนวณจำนวนต่างๆ โดยการคูณเลขหลายหลักอาจจะต้องใช้เวลาในการหาผลลัพธ์นั้นค่อนข้างนาน แต่ตัวเลขที่เรานำไปคูณบางตัวนั้นก็มีเทคนิควิธีลัดในการคิดหาผลลัพธ์ ทำให้เราใช้เวลาคิดเพียงเล็กน้อย ได้ผลลัพธ์รวดเร็ว

- การคูณเลขด้วย 9, 99,999…

วิธีคิด 1. ให้นำ 1 บวกกับจำนวนที่ลงท้ายด้วย 9

2. จากนั้นนำไปคูณกับจำนวนที่คูณกับ 9 , 99 , 999… เช่น 45 x 99 ก็ต้องเอา 100 มาคูณ 45 เป็น 4,500 แล้วนำมาลบกับ 45 ก็จะได้คำตอบ

ตัวอย่าง การคูณด้วย 9, 99, 999...

1. 748 x 9 = 7,480 - 748 = 6,732

2. 543 x 99 = 54,300 - 543 = 53,757

3. 8,965 x 999 = 8,965,000 – 8,965 = 8,956,035 เป็นต้น

ยกตัวอย่างจากข้อสาม 8,965 x 999 ?

นำ 1 บวกกับ 999 ได้ 1,000

จากนั้นนำไปคูณ 8,965 x 1,000 = 8,965,000

แล้วลบด้วย 8,965 อีกครั้งหนึ่ง คือ 8,965,000 – 8,965 = 8,956,035

ผลลัพธ์ที่ได้ คือ 8,956,035

- กการคูณเลขด้วย 11

แบบที่ 1 คือ จำนวน 2 หลักที่คูณด้วยเลข 11

วิธีคิด 1. นำตัวเลขสองหลักนั้นมาเขียนใหม่โดยเว้นช่องตรงกลางเอาไว้

2. ช่องตรงกลางคือ ผลบวกของตัวมันเอง

ตัวอย่างที่ 1 52 x 11 = ?

วิธีทำ 1. 52 x 11 = 5_2 (นำตัวเลขสองหลักนั้นมาเขียนใหม่โดยเว้นช่องตรงกลางเอาไว้)

2. นำ 5+2=7 นำ 7 มาไว้ตรงกลาง) ก็จะได้คำตอบ 572

ตอบ 572

ตัวอย่างที่ 2 83 x 11 = ?

วิธีทำ 1. 83 x 11 = 8_3 (นำตัวเลขสองหลักนั้นมาเขียนใหม่โดยเว้นช่องตรงกลางเอาไว้)

ในกรณีที่จำนวนของผลบวกนั้นมี 2 หลัก ให้นำหลักหน่วยใส่ไว้ตรงกลาง และนำหลักสิบทดไว้ที่เลขตัวข้างหน้าทางซ้ายมือ แล้วนำเลขทางซ้ายบวกกับจำนวนที่ทดไว้ คือ 8+1 = 9

ตอบ 913

แบบที่ 2 จำนวนหลายๆหลักที่คูณด้วยเลข 11

วิธีคิด 1. นำ 0 ไปเติมไว้ทั้งหน้าและหลัง จำนวน แล้วนำมาบวกกัน

เช่น 123 x 11 จะได้ 01230 แล้วนำมาบวกกัน ตามรูป

ตอบ 1,353

- การคูณเลขด้วย 25

วิธีคิด 1. นำจำนวนที่คูณด้วย 25 มาเติม 00 เช่น 48 x 25 ให้เอา 48 มาเติม 00 จะได้ 4,800

2. นำ 4 มาหาร 4,800 จะได้ 1,200 เป็นคำตอบ ดังนั้น 48 x 25 = 1,200

ตัวอย่างที่ 1 357 x 25 = ?

วิธีทำ 357x 25 = 35,700

= 35,700 แล้วนำมาหารหารด้วย 4

= 8,925

ตอบ 8,925

ที่มา http://gotoknow.org/blog/tiwanporn3/268122

http://math-tiger.blogspot.com/2010_11_01_archive.html

รูปเรขาคณิต / รูปทรงเรขาคณิต

รูปเรขาคณิต

รูป เรขาคณิต หมายถึง รูปต่างๆ ทางเรขาคณิต เช่น

รูปสามเหลี่ยม มีด้าน 3 ด้าน มีมุม 3 มุม

รูปสี่เหลี่ยม มีด้าน 4 ด้าน มีมุม 4 มุม

รูปห้าเหลี่ยม มีด้าน 5 ด้าน มีมุม 5 มุม

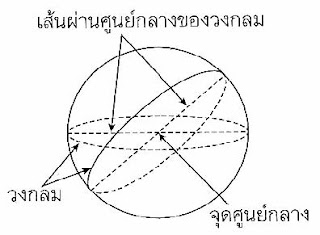
รูปหกเหลี่ยม มีด้าน 6 ด้าน มีมุม 6 มุม

รูปวงกลม มีเส้นโค้งเป็นวงกลม และห่างจากจุดศูนย์กลางเป็นระยะทางเท่ากัน

รูปวงรี มีเส้นเส้นโค้งเป็นวงรี โดยห่างจากจุดศูนย์กลางไม่เท่ากัน

รูปทรง เรขาคณิตรูปทรงเรขาคณิต หมายถึง รูปที่มีส่วนที่เป็นพื้นผิว ส่วนสูง และส่วนลึก หรือหนา

รูปทรงกลม

รูปทรงสี่เหลี่ยมมุมฉาก

รูปทรงกระบอก

รูปเรขาคณิตสามมิติระดับชั้นมัธยมต้นนี้ นักเรียนควรมีพื้นฐานเกี่ยวกับ พื้นที่ผิวและปริมาตรที่ควรทราบ ดังนี้

ปริซึม

ปริซึม เป็นรูปเรขาคณิตสามมิติที่มีหน้าตัด(ฐาน) ทั้งสองข้างเป็นรูปหลายเหลี่ยมที่เท่ากันทุกประการหน้าตัด (ฐาน) ทั้งสองอยู่ในระนาบที่ขนานกัน มีหน้าข้างเป็นรูปสี่เหลี่ยมมุมฉาก การเรียกชื่อปริซึมจะเรียกตามรูปหน้าตัดของปริซึมส่วนต่างๆของปริซึมมีชื่อเรียก ดังนี้

ทรงกระบอก

ทรงกระบอก เป็นรูปเรขาคณิตสามมิติที่มีฐานสองฐานเป็นรูปวงกลมที่เท่ากันทุกประการและอยู่บนระนาบที่ขนานกัน และเมื่อตัดรูปเรขาคณิตสามมิตินั้นด้วยระนาบที่ขนานกับฐานแล้ว จะได้หน้าตัดเป็นวงกลมที่เท่ากันทุกประการกันฐานเสมอ ด้านข้างเป็นผิวเรียบโค้งส่วนต่างๆของทรงกระบอก
ข้อแตกต่างของปริซึมกับทรงกระบอก คือ
- ฐาน ปริซึมเป็นรูปหลายเหลี่ยมทรงกระบอกเป็นวงกลม- ด้านข้าง ปริซึมเป็นรูปสี่เหลี่ยมผืนผ้าทรงกระบอกเป็นผิวเรียบโค้ง

พีระมิด

พีระมิด เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปเหลี่ยมใดๆ มียอดแหลมที่ไม่อยุ่บนระนาบเดียวกันกับฐาน และหน้าทุกหน้าเป็นรูปสามเหลี่ยมที่มีจุดยอดร่วมกันที่ยอดแหลมนั้น การเรียกชื่อพีระมิดจะเรียdตามรูปฐานของพีระมิด

กรวย
กรวย เป็นรูปเรขาคณิตสามมิติที่มีฐานเป็นรูปวงกลม มียอดแหลมที่ไม่อยู่ในระนาบเดียวกันกับฐาน และเส้นที่ต่อระหว่างจุดยอดกับจุดใดๆ บนขอบของฐานเป็นส่วนของเส้นตรงดด้านข้างเป็นผิวโค้งเรียบระมิ
ส่วนต่างๆของกรวย
ข้อแตกต่างของพีระมิดกับกรวย คือ- ฐาน พีระมิดฐานรูปหลายเหลี่ยมกรวยฐานรูปวงกลม
- ด้านข้าง พีระมิดเป็นรูปสามเหลี่ยมผืนผ้า
กรวยเป็นผิวเรียบโค้ง

ทรงกลม

ทรงกลม เป็น รูปเรขาคณิตสามมิติที่มีด้านข้างเป็นผิวโค้งเรียบ และจุดทุกจุดบนผิวโค้งอยู่ห่างจากจุดคงที่จุดหนึ่งเป็นระยะเท่ากัน เรียกจุดคงที่ว่า จุดศูนย์กลางของทรงกลม
เรียกระยะที่เท่ากันว่า รัศมีของทรงกลม
ส่วนต่างๆของทรงกลม

ที่มา:http://math-tiger.blogspot.com/2010/05/blog-post.html

วันจันทร์ที่ 9 มกราคม พ.ศ. 2555

เทคนิคการบวกเลขเร็ว

เทคนิคการบวกเลขเร็ว

ที่เริ่มจาก 1

                ให้ใช้สูตร [ (1 + ตัวท้าย) ตัวท้าย] หาร 2 = ผลลัพธ์
        หรือใช้สูตรโบราณว่า    "เอา 1 บวกเข้า    เอาเก่ามาคูณ   เอา 2 หารตัด ขาดลงเป็นผลลัพธ์"
ตัวอย่าง เช่น
               บวกเลขเรียงจาก 1 ถึง 200
                 (1+200)*200   =20,100
                        2
            ดังนั้น บวกเลขเรียงจาก 1 ถึง 200 = 20,100

ลองคิดดูเล่นๆ ค่ะ
1. 1 ถึง 10    =   .................. (55)
2. 1 ถึง 80    = ...................   (3,240)
3. 1 ถึง 500 = ...................   (125,250)

ที่ไม่เริ่มจาก 1

1. บวกเลขเรียงจาก 1 ถึงตัวท้ายโดยใช้สูตร    (1 + ตัวท้าย) ตัวท้าย 2 = ตัวตั้ง
2. บวกเลขเรียงจาก 1 ถึงตัวก่อนเริ่มใช้สูตร คือ (1 + ตัวก่อนเริ่ม) ตัวก่อนเริ่ม 2 = ตัวลบ
3. เอาผลลัพธ์ที่ได้จาก ข้อ 1 - 2 เป็นผลบวกเลขเรียงที่ไม่เริ่มต้นจาก 1
ตัวอย่าง เช่น
               บวกเลขเรียงจาก 9 ถึง 20
                     บวกเลขเรียงจาก 1 ถึง 20 ได้ 210 เป็นตัวตั้ง
                     บวกเลขเรียงจาก 1 ถึง 8   ได้   36 เป็นตัวลบ
            ดังนั้น บวกเลขเรียงจาก 9 ถึง 20 = 210 - 36 = 174

ลองคิดดูเล่นๆ ค่ะ
1. 6 ถึง 10    =   .................. (40)
2. 12 ถึง 30    = ...................   (399)
3. 55 ถึง 80  = ...................   (1,755)

คี่จำนวน

ให้หาตัวกลางของจำนวนที่บวกกันนั้น คูณกับจำนวนที่ให้บวกกันทั้งหมด
ตัวอย่าง เช่น
               97 + 98 + 99 + 100 + 101 = .............................
               สังเกตพบว่่าจำนวนที่ให้บวกกันนั้นทั้งหมดมี 5 จำนวน และตัวกลางของจำนวนเหล่านี้คือ 99
               ให้เอา 5 99 = 495
   ดังนั้น 97 + 98 + 99 + 100 + 101 = 495
ลองคิดดูเล่นๆ ค่ะ
1. 15 + 16 + 17    =   .................. (48)
2. 125 + 126 + 127 + 128 129    = ...................   (635)
3. 63 + 64 + 65 + 66 + 67 + 68 + 69 + 70 + 71  = ...................   (603)

คู่จำนวน

ให้หาตัวกลางของจำนวนที่บวกกันนั้น คูณกับจำนวนที่ให้บวกกันทั้งหมด ซึ่งตัวกลางมี 2 จำนวน ให้เอาตัวกลาง 2 จำนวนนั้นบวกกันแล้วเอา 2 หารได้ผลลัพธ์เท่าไร คูณกับจำนวนที่ให้บวกกันทั้งหมด ก็จะได้ผลลัพธ์ที่ถูกต้องและรวดเร็ว
ตัวอย่าง เช่น
               97 + 98 + 99 + 100 + 101+ 102 = .............................
               สังเกตพบว่่าจำนวนที่ให้บวกกันนั้นทั้งหมดมี 6 จำนวน และตัวกลางของจำนวนเหล่านี้คือ (99 + 100) 2 = 99.5
               ให้เอา 6 99.5 = 597
   ดังนั้น 97 + 98 + 99 + 100 + 101+ 102 = 597
ลองคิดดูเล่นๆ ค่ะ
1. 15 + 16 + 17 + 18    =   .................. (66)
2. 125 + 126 + 127 + 128 129 + 130   = ...................   (765)
3. 63 + 64 + 65 + 66 + 67 + 68 + 69 + 70 + 71+ 72  = ...................   (675)

ที่มา : http://www.thaigoodview.com/library/teachershow/lopburi/benja_j/easy_math/index.html

จัดทำโดยครูเบ็ญจ ใจการุณ โรงเรียนบ้านหลุมข้าว อำเภอโคกสำโรง จังหวัดลพบุรี 15120

(1+200)*200 =20,100
2